
Издательство «Бомбора» представляет книгу Кита Йейтса «Математика жизни и смерти. Семь математических принципов, формирующих нашу жизнь».
Семь глав этой книги исследуют подлинные истории из жизни, в которых корректное (или некорректное) применение математики сыграло решающую роль. Это истории болезней, вызванных дефектными генами; истории банкротств, вызванных применением ошибочных алгоритмов; истории невинных жертв судебных ошибок и нечаянных жертв сбоев в работе программного обеспечения. Мы проследим за историями инвесторов, потерявших состояние, и родителей, потерявших детей, — и всё из-за математических недоразумений. Мы столкнемся с этическими дилеммами — от проверок благонадежности до манипулирования статистикой; исследуем общественные проблемы — политические референдумы, профилактику заболеваний, уголовное правосудие и искусственный интеллект. Это не учебник математики. И это не книга для математиков. Вы не найдете здесь ни одного уравнения. Смысл книги не в том, чтобы напомнить об уроках математики, которые вы посещали, вероятно, очень-очень давно. Совсем наоборот. Если когда-то вы разочаровались в математике и решили, что она — не для вас, что она вам не дается, эта книга избавит вас от таких комплексов.
Предлагаем прочитать фрагмент книги.
Математические законы
73 миллиона к одному
Во время суда над Салли Кларк противоречивые доказательства мешали присяжным принять однозначное решение. Салли твердила, что она не убивала своих детей. Патологоанатом Министерства внутренних дел и свидетель-эксперт обвинения, доктор Алан Уильямс, утверждал обратное. Медицинская экспертиза, которую он представил, была запутанной и слишком сложной для присяжных. Во время подготовки к судебному процессу независимые эксперты легко дискредитировали разрывы в тканях мозга, повреждения позвоночника и кровоизлияния в сетчатку, которые Уильямс первоначально «обнаружил» при вскрытии Гарри. В результате обвинение изменило позицию и попыталось убедить присяжных в том, что Гарри задушили, а не затрясли до смерти, как утверждалось первоначально. Даже Уильямс передумал. Экспертно-медицинские заключения были исключительно туманны и неоднозначны.
Ожесточенная борьба между защитой и обвинением вокруг косвенных улик, связанных с этими двумя смертями, запутала ситуацию еще сильнее. Обвинение изображало Салли тщеславной и эгоистичной карьеристкой, раздраженной тем, как изменились ее образ жизни и ее тело после рождения детей. Женщиной, которая так отчаянно стремилась вернуться к своей прежней, бездетной жизни, что убила своих малышей. Почему же тогда, возражала защита, она так быстро родила второго ребенка? И почему она вновь забеременела и родила третьего, пока шла подготовка к суду? Защита утверждала, что Салли была явно опечалена смертью своего первого сына. Сторона обвинения пыталась использовать аргумент в свою пользу, намекая, что в таком демонстративном горе было что-то подозрительное. Врач, впервые увидевший Кристофера, когда тот приехал в больницу, возразил, что в отчаянии Салли не было ничего необычного — это естественная реакция на потерю первенца. Стороны перебрасывались аргументами, как воланчиком в бадминтоне, и у присяжных голова шла кругом.
Среди этой путаницы в дело вступил свидетель-эксперт, профессор сэр Рой Мидоу. В то время как патологи спорили о степени «легочного кровотечения» и «субдуральных гематом», Мидоу вел присяжных от подводных скал замешательства к спокойным водам вердикта, на яркий свет маяка статистики. Он оперировал единственным показателем, постулировавшим, что вероятность синдрома внезапной детской смерти (СВДС, который также часто называют смертью в колыбели) у двух подряд детей из обеспеченной семьи составляет 1 на 73 миллиона. Для многих присяжных это оказалась самая важная информация, которую они извлекли из процесса: 73 миллиона было слишком большим числом, чтобы его игнорировать.
В 1989 году под редакцией Мидоу, уже тогда известного британского педиатра, вышла книга «Азбука жестокого обращения с детьми». В ней был постулат, который позже назвали «законом Мидоу»: «Одна внезапная детская смерть — трагедия, две — уже повод для подозрений, а три — убийство, пока не будет доказано обратное». Однако эта бойкая сентенция основана на фундаментальном непонимании природы вероятности. С помощью такого же ложного представления о вероятности — разнице между зависимыми и независимыми событиями — Мидоу ввел в заблуждение и присяжных в случае с Салли Кларк.
Ошибка независимости
Два события считаются зависимыми, если знание о том, что произошло одно из них, влияет на вероятность происхождения другого. В противном случае они независимы. Для расчета вероятности того, что произойдет комбинация нескольких событий, обычно перемножают вероятности происхождения каждого из них. Так, шанс, что случайно выбранный из населения человек является женщиной, составляет ½. Как показано в табл. 3, из 1000 человек в среднем 500 будут женщинами. Вероятность того, что у случайно выбранного человека из числа всего населения коэффициент IQ будет больше 110 баллов, составляет ¼ (таким образом, из 1000 человек такой результат покажут 250 — см. таблицу 3). Чтобы выяснить вероятность того, что произвольно выбранная женщина обладает IQ выше 110, мы перемножаем вероятности ½ и ¼, что дает вероятность 1/8 (и соответствует количеству 125 (1000/8) человек в подгруппе женщин с высоким IQ в табл. 3). Это прекрасный пример такой методологии, поскольку показатель IQ и половая принадлежность абсолютно независимы: наличие определенного IQ ничего не говорит о вашем поле, а принадлежность к определенному полу ничего не говорит о вашем IQ.

Табл. 3. Распределение 1000 человек по показателю IQ и половой принадлежности
Распространенность аутизма в Великобритании составляет примерно 1 на 100, или, соответственно, 10 на 1000. Действуя по описанной выше логике, можно предположить, что для определения вероятности того, что произвольно взятая женщина будет страдать аутизмом, надо просто перемножить две вероятности (1/2 и 1/100), что в итоге даст 1/200, то есть распространенность составит 5 случаев на 1000 человек. Однако аутизм и пол не являются независимыми вероятностями. При анализе 1000 случайно выбранных людей в популяции, как показано в табл. 4, мы увидим, что вероятность аутизма у мужчин в четыре раза выше (8 на 500), чем у женщин (2 на 500). Только 1 из 5 человек, страдающих аутизмом, будет женщиной. Нам нужна эта дополнительная информация, чтобы корректно вычислить вероятность того, что случайно выбранный человек в популяции будет и женщиной, и аутистом одновременно. Верное значение этой вероятности составит 2/1000, а не 5/1000, что мы получили бы, ошибочно предположив независимость отдельных вероятностей. Пример демонстрирует, как легко совершить серьезные ошибки, опираясь на неверные предположения о независимости событий.
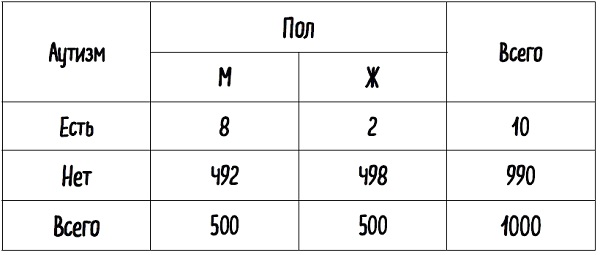
Табл. 4. Распределение 1000 человек по половой принадлежности и наличию аутизма
В своих показаниях Мидоу рассматривал смерти детей Салли Кларк в результате СВДС как отдельные вероятностные события. В вычислениях он опирался на данные тогда еще не опубликованного доклада о синдроме внезапной детской смерти, для которого ему предложили написать предисловие. В докладе на материале английской статистики было изучено 363 случая СВДС, пришедшихся на общее число в 473 родившихся живыми младенцев за трехлетний период. Наряду с общей частотой внезапной детской смертности по всему населению доклад представил распределение данных по возрасту матерей, доходам домохозяйств, а также по тому, курил ли кто-либо из членов семьи. В обеспеченных некурящих семьях с матерью старше 26 лет — таких как семья Кларк — на каждые 8543 живорожденных приходился всего один случай СВДС.
Первой ошибкой Мидоу было предположение, что случаи синдрома внезапной детской смерти являются полностью независимыми событиями. Эта ложная посылка позволила ему при расчете вероятности того, что смерть двух детей в одной семье будет вызвана СВДС, просто перемножить число 8543 на самое себя. В результате он получил, что вероятность такого события составит примерно 1 на каждые 73 миллиона удачных родов. Пытаясь обосновать свои предположения, он даже заявил: «Нет никаких доказательств того, что "смерти в колыбели" происходят в семьях серийно, зато серийному жестокому обращению с детьми доказательств множество». С этой цифрой на руках он предположил, что при уровне рождаемости в Великобритании, составляющем около 700 тысяч человек в год, две подряд «смерти в колыбели» можно было бы ожидать примерно раз в 100 лет.
Его допущение было исключительно некорректным. Известно много факторов повышения риска СВДС. В их число входят курение, преждевременные роды и даже сон в одной постели с родителями. В 2001 году исследователи Манчестерского университета выделили генетические маркеры, связанные с регулированием иммунной системы, которые также повышают риск СВДС. С тех пор обнаружили множество других генетических факторов, также увеличивающих вероятность СВДС. У родных братьев и сестер много общих генов — соответственно, риск развития СВДС у них выше. Если от СВДС умирает один ребенок, то вполне вероятно, что в семье действуют какие-то сопутствующие факторы риска. Следовательно, вероятность второй смерти в такой семье будет выше, чем в среднем по населению. В действительности считается, что в Великобритании ежегодно происходит хотя бы один случай СВДС у второго ребенка.
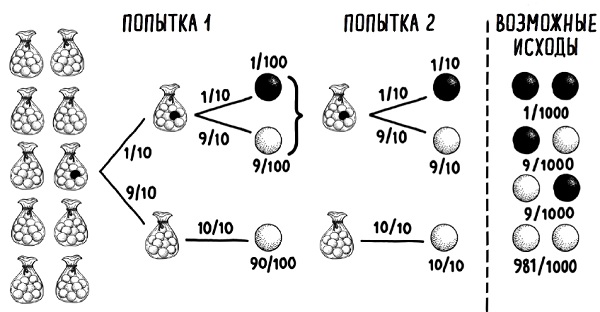
Рис. 9. Древо решений для поиска вероятности выбора черных или белых шариков. Для вычисления вероятности выбора черного или белого шарика при каждой попытке следуйте за соответствующими ветвями древа и умножайте вероятности на каждом шаге. Так, вероятность вытащить черный шарик с первой попытки составляет 1/100. При второй попытке мы выбираем из того же мешка, который мы выбрали при первой попытке. Вероятности каждой комбинации из двух вариантов показаны справа от пунктирной линии
Давайте смоделируем ситуацию, в которой мы сможем вычислить аналог вероятности смерти от СВДС. Возьмем десять мешочков с мраморными шариками. В девяти таких мешочках по десять белых шариков. В десятом же — девять белых и один черный. Эти стартовые условия представлены слева на рис. 9. На первом шаге вы выбираете произвольный мешок, а в нем — произвольный шарик. Поскольку шариков всего 100 и выбор любого из них одинаково возможен, вероятность выбора черного шарика на первом шаге составляет 1 из 100. На втором шаге вы возвращаете шарик обратно в тот же мешочек и вытаскиваете из него же еще один, игнорируя остальные мешочки. Если на первом шаге вы вытянули черный шарик, то вы знаете, что и во второй раз выбираете из набора, в котором этот шарик точно есть. Это значительно повышает вероятность выбора черного шарика — до 1 из 10, а не 1 из 100. В этом сценарии выбор двух черных шариков подряд (с вероятностью 1 к 1000) намного более вероятен, чем при простом перемножении исходной вероятности выбора одного черного шарика на саму себя (что даст вероятность удачного исхода в 1 к 10 000). В случае с вероятностью смерти второго ребенка от СВДС, если первый умер от этого синдрома, математика аналогична — вероятность растет.
При реальном расчете угрозы СВДС факторы риска для каждой семьи не выбираются случайным образом из всего их многообразия; они уже заданы заранее — можно утверждать, что с самого начала вы либо выбираете из мешочка с черным шариком в нем, либо из другого, в котором черного шарика заведомо нет. Эта альтернативная интерпретация проиллюстрирована в виде двух деревьев принятия решений на рис. 10. Если вам достался мешочек с черным шариком в обоих случаях, то вероятность выбора двух черных шариков возрастает до 1 к 100. Таким образом очевидно, что простое перемножение общепопуляционного фактора фонового риска развития СВДС на самого себя при вычислении вероятности развития СВДС для конкретного случая — некорректный прием.
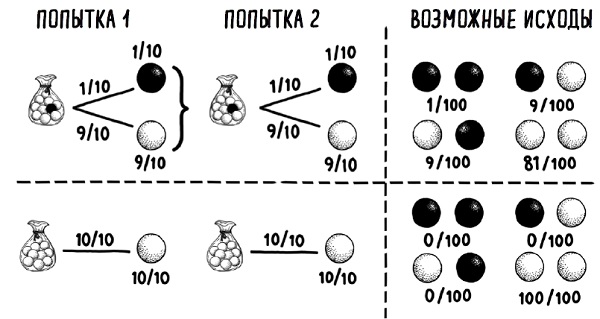
Рис. 10. Два альтернативных древа принятия решений, где мешочек, из которого вы выбираете, жестко задан заранее для обеих попыток выбора. Для каждого древа вероятность выпадения каждой из двухвариантных комбинаций выбора показана справа от пунктирной линии. Очевидно, что если мы выбираем из мешочка, где черного шарика нет, то единственная возможность — это выпадение двух белых шариков
Тенденциозный подход Мидоу, опиравшегося на общий показатель 1 случай смерти от СВДС на 8543 случая живорождения, имел и другие слабые места. Отчет, из которого он выбрал этот показатель, предлагал и другую, гораздо более высокую общепопуляционную оценку риска — 1 к 1303 (этот показатель был рассчитан без разделения данных по социально-экономическим факторам). Мидоу решил не использовать эту альтернативную оценку. Вместо того, сделав особый акцент на условиях жизни семьи Кларк, Мидоу вывел значение, согласно которому вероятность даже одного случая СВДС выглядела гораздо ниже (а поскольку он безосновательно проигнорировал зависимость между серийными смертями от СВДС, повторная смерть от этого синдрома выглядела еще менее вероятной), пренебрегая теми факторами, которые делали его гораздо более вероятным. Так, он проигнорировал тот факт, что оба ребенка Салли были мальчиками и что СВДС у мальчиков развивается почти в два раза чаще, чем у девочек. Учет этого фактора подорвал бы позиции обвинения, показав более высокую вероятность серийной смерти от СВДС. В этом свете шанс, что Салли убила двух своих детей, представляется соразмерно ниже.
Хотя тенденциозный подбор стороной обвинения статистических данных сам по себе мог бы считаться неэтичным или даже заведомо ложным, подобная практика порождает куда более серьезную проблему. Классификация данных в докладе, на который опирался Мидоу, была проведена, чтобы выявить категории населения, наиболее подверженные высоким рискам и более эффективно использовать ограниченные ресурсы системы здравоохранения. Она никогда не предназначалась для того, чтобы делать выводы о риске развития СВДС в каждом конкретном случае — даже в этих группах повышенного риска. Доклад представлял собой самое общее исследование почти полумиллиона родов в Великобритании, а при таком исследовании индивидуальные обстоятельства каждых родов детально изучить невозможно (да и цели такой обычно не ставится). Дело же Салли Кларк, напротив, было чрезвычайно подробным расследованием конкретного случая. Обвинение выбрало только те аспекты биографии Салли и Стива, которые подходили под нарисованную в отчете картину, и, без учета других факторов, решило использовать эту конструкцию для определения степени риска развития СВДС у детей четы Кларк. Однако такой подход основан на ложном допущении о том, что индивидуальные характеристики тождественны характеристикам населения. Это классический пример так называемой экологической ошибки.
